| Extended content |
|---|
|
Template:Other uses Template:Refimprove  A monk (from Template:Lang-el, monachos, "single, solitary" and Latin monachus[1]) is a person who practices religious asceticism, living either alone or with any number of other monks. A monk may be a person who decided to dedicate his life to serving all other living beings, or to be an ascetic who voluntarily chooses to leave mainstream society and live his life in prayer and contemplation. The concept is ancient and can be seen in many religions and in philosophy. In the Greek language the term can apply to women, but in modern English it is mainly in use for men. Meanwhile, nun is typically used for female monastics. Although the term monachos is of Christian origin, in the English language "monk" tends to be used loosely also for both male and female ascetics from other religious or philosophical backgrounds. However, being generic, it is not interchangeable with terms that denote particular kinds of monk, such as friar, cenobite, hermit, anchorite, hesychast, or solitary. Eastern Christianity In the Eastern Orthodoxy and Oriental Orthodoxy monasticism holds a very special and important place: "Angels are a light for monks, monks are a light for laymen" (St. John Klimakos). The Orthodox Church measures its health by the quality of its monks and nuns. Orthodox monastics separate themselves from the world in order to pray unceasingly for the world. They do not, in general, have as their primary purpose the running of social services, as is common in Western Christianity, but instead are concerned with attaining theosis, or union with God. However, care for the poor and needy has always been an obligation of monasticism,[citation needed] so Orthodox monasteries are not normally "cloistered" like some contemplative Western houses are, though the level of contact will vary from community to community. Orthodox hermits, on the other hand, have little or no contact with the outside world. Orthodox monasticism does not have religious orders as are found in the West, nor do they have Rules in the same sense as the Rule of St. Benedict. Rather, Eastern monastics study and draw inspiration from the writings of the Desert Fathers as well as other Church Fathers; probably the most influential of which are the Greater Asketikon and Lesser Asketikon of St. Basil the Great and the Philokalia, which was compiled by St. Nikodemos of the Holy Mountain and St. Makarios of Corinth. Hesychasm is of primary importance in the ascetical theology of the Orthodox Church.  Most communities are self-supporting, and the monastic’s daily life is usually divided into three parts: (a) communal worship in the catholicon (the monastery's main church); (b) hard manual labour; and (c) private prayer, spiritual study, and rest when necessary. Meals are usually taken in common in a sizable dining hall known as a trapeza (refectory), at elongated refectory tables. Food is usually simple and is eaten in silence while one of the brethren reads aloud from the spiritual writings of the Holy Fathers. The monastic lifestyle takes a great deal of serious commitment. Within the cenobitic community, all monks conform to a common way of living based on the traditions of that particular monastery. In struggling to attain this conformity, the monastic comes to realize his own shortcomings and is guided by his spiritual father in how to deal honestly with them. Attaining this level of self-discipline is perhaps the most difficult and painful accomplishment any human being can make; but the end goal, to become like an angel on earth (an "earthly angel and a heavenly man", as the church hymns put it), is the reason monastics are held in such high esteem. For this same reason, bishops are almost always chosen from the ranks of monks. Eastern monasticism is found in three distinct forms: anchoritic (a solitary living in isolation), cenobitic (a community living and worshiping together under the direct rule of an abbot or abbess), and the "middle way" between the two, known as the skete (a community of individuals living separately but in close proximity to one another, who come together only on Sundays and feast days, working and praying the rest of the time in solitude, but under the direction of an elder). One normally enters a cenobitic community first, and only after testing and spiritual growth would one go on to the skete or, for the most advanced, become a solitary anchorite. However, one is not necessarily expected to join a skete or become a solitary; most monastics remain in the cenobuim the whole of their lives. In general, Orthodox monastics have little or no contact with the outside world, including their own families. The purpose of the monastic life is union with God, the means is through leaving the world (i.e., the life of the passions). After tonsure, Orthodox monks and nuns are never permitted to cut their hair. The hair of the head and the beard remain uncut as a symbol of the vows they have taken, reminiscent of the Nazarites from the Old Testament. The tonsure of monks is the token of a consecrated life, and symbolizes the cutting off of their self-will. DegreesSee also: Degrees of Eastern Orthodox monasticism
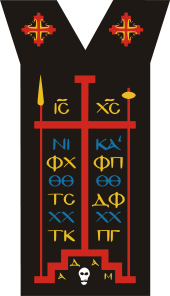 The process of becoming a monk is intentionally slow, as the vows taken are considered to entail a lifelong commitment to God, and are not to be entered into lightly. In Orthodox monasticism after completing the novitiate, there are three ranks of monasticism. There is only one monastic habit in the Eastern Church (with certain slight regional variations), and it is the same for both monks and nuns. Each successive grade is given a portion of the habit, the full habit being worn only by those in the highest grade, known for that reason as the "Great Schema", or "Great Habit". The various profession rites are normally performed by the Abbot, but if the abbot has not been ordained a priest, or if the monastic community is a convent, a hieromonk will perform the service. The abbot or hieromonk who performs a tonsure must be of at least the rank he is tonsuring into. In other words, only a hieromonk who has been tonsured into the Great Schema may himself tonsure a Schemamonk. A bishop, however, may tonsure into any rank, regardless of his own. Novice (Church Slavonic: Poslushnik), lit. "one under obedience"—Those wishing to join a monastery begin their lives as novices. After coming to the monastery and living as a guest for not less than three days, the revered abbot or abbess may bless the candidate to become a novice. There is no formal ceremony for the clothing of a novice, he or she simply receives permission to wear the clothing of a novice. In the Eastern monastic tradition, novices may or may not dress in the black inner cassock (Greek: Anterion, Eisorasson; Church Slavonic: Podriasnik) and wear the soft monastic hat (Greek: Skoufos, Church Slavonic: Skufia), depending on the tradition of the local community, and in accordance to the abbot’s directives. The inner-cassock and the skoufos are the first part of the Orthodox monastic habit. In some communities, the novice also wears the leather belt. He is also given a prayer rope and instructed in the use of the Jesus Prayer. If a novice chooses to leave during the period of the novitiate, no penalty is incurred. He may also be asked to leave at any time if his behaviour does not conform to the monastic life, or if the superior discerns that he is not called to monasticism. When the abbot or abbess deems the novice ready, he is asked if he wishes to join the monastery. Some, out of humility, will choose to remain novices all their lives. Every stage of the monastic life must be entered into voluntarily. Rassophore (Church Slavonic: Ryassofor), lit. "Robe-bearer"—If the novice continues on to become a monk, he is clothed in the first degree of monasticism at a formal service known as the Tonsure. Although there are no formal vows made at this point, the candidate is normally required to affirm his commitment to persevere in the monastic life. The abbot will then perform the tonsure, cutting a small amount of hair from four spots on the head, forming a cross. He is then given the outer cassock (Greek: Rasson, Exorasson, or Mandorasson; Church Slavonic: Ryassa)—an outer robe with wide sleeves, something like the cowl used in the West, but without a hood—from which the name of Rassophore is derived. He is also given a brimless hat with a veil, known as a klobuk, and a leather belt is fastened around his waist. His habit is usually black, signifying that he is now dead to the world, and he receives a new name. Although the Rassophore does not make formal vows, he is still morally obligated to continue in the monastic estate for the rest of his life. Some will remain Rassophores permanently without going on to the higher degrees. Stavrophore (Church Slavonic: Krestonosets), lit. "Cross-bearer"—The next level for Eastern monastics takes place some years after the first tonsure when the abbot feels the monk has reached an appropriate level of discipline, dedication, and humility. This degree is also known as the Little Schema, and is considered to be a "betrothal" to the Great Schema. At this stage, the monk makes formal vows of stability, chastity, obedience and poverty. Then he is tonsured and clothed in the habit, which in addition to that worn by the Rassophore, includes the paramandyas (Church Slavonic: paraman), a piece of square cloth worn on the back, embroidered with the instruments of the Passion (see picture above), and connected by ties to a wooden cross worn over the heart. The paramandyas represents the yoke of Christ. Because of this addition he is now called Stavrophore, or Cross-bearer. He is also given a wooden hand cross (or "profession cross"), which he should keep in his icon corner, and a beeswax candle, symbolic of monastic vigilance the sacrificing of himself for God. He will be buried holding the cross, and the candle will be burned at his funeral. In the Slavic practice, the Stavrophore also wears the monastic mantle. The rasson (outer robe) worn by the Stavrophore is more ample than that worn by the Rassophore. The abbot increases the Stavrophore monk’s prayer rule, allows a more strict personal ascetic practice, and gives the monk more responsibility. Great Schema (Greek: Megaloschemos, Church Slavonic: Skhimnik)—Monks whose abbot feels they have reached a high level of spiritual excellence reach the final stage, called the Great Schema. The tonsure of a Schemamonk follows the same format as the Stavrophore, and he makes the same vows and is tonsured in the same manner. But in addition to all the garments worn by the Stavrophore, he is given the Analavos (Church Slavonic: Analav) which is the article of monastic vesture emblematic of the Great Schema. For this reason, the analavos itself is sometimes called the "Great Schema". The analavos comes down in the front and the back, somewhat like the scapular in Western monasticism, although the two garments are probably not related. It is often intricately embroidered with the instruments of the Passion and the Trisagion (the angelic hymn). The Greek form does not have a hood, the Slavic form has a hood and lappets on the shoulders, so that the garment forms a large cross covering the monk's shoulders, chest, and back. Another piece added is the Polystavrion or "Many Crosses", which consists of a cord with a number of small crosses plaited into it. The polystavrion forms a yoke around the monk and serves to hold the analavos in place, and reminds the monastic that he is bound to Christ and that his arms are no longer fit for worldly activities, but that he must labor only for the Kingdom of Heaven. Among the Greeks, the mantle is added at this stage. The paramandyas of the Megaloschemos is larger than that of the Stavrophore, and if he wears the klobuk, it is of a distinctive thimble shape, called a koukoulion, the veil of which is usually embroidered with crosses. In some monastic traditions the Great Schema is only given to monks and nuns on their death bed, while in others they may be elevated after as little as 25 years of service. Eastern Orthodox monks are addressed as "Father" even if they are not priests; but when conversing among themselves, monks will often address one another as "Brother". Novices are always referred to as "Brother". Among the Greeks, old monks are often called Gheronda, or "Elder", out of respect for their dedication. In the Slavic tradition, the title of Elder (Church Slavonic: Starets) is normally reserved for those who are of an advanced spiritual life, and who serve as guides to others. For the Orthodox, Mother is the correct term for nuns who have been tonsured Stavrophore or higher. Novices and Rassophores are addressed as "Sister". Nuns live identical ascetic lives to their male counterparts and are therefore also called monachai (the feminine plural of monachos), and their community is likewise called a monastery. Many (but not all) Orthodox seminaries are attached to monasteries, combining academic preparation for ordination with participation in the community's life of prayer, and hopefully benefiting from the example and wise counsel of the monks. Bishops are required by the sacred canons of the Orthodox Church to be chosen from among the monastic clergy. It should be noted that the requirement is specifically that they be monastics, not simply celibate (see clerical celibacy). Monks who have been ordained to the priesthood are called hieromonks (priest-monks); monks who have been ordained to the diaconate are called hierodeacons (deacon-monks). A Schemamonk who is a priest is called a Hieroschemamonk. Most monks are not ordained; a community will normally only present as many candidates for ordination to the bishop as the liturgical needs of the community require. Western ChristianityRoman Catholicism  Within Roman Catholicism, a monk is a member of a religious order who lives a communal life in a monastery, abbey, or priory under a monastic rule of life (such as the Rule of St. Benedict). St. Benedict of Nursia is considered to be the founder of western monasticism. He authored the Rule of St. Benedict, which is the foundation for the Order of St. Benedict and all of its reform groups such as the Cistercians and the Trappists. The religious vows taken in the West were first developed by St. Benedict. These vows were three in number: obedience, conversion of life, and stability. Obedience calls for the monk to obey Christ, as represented by the superior person of the monastery, which is an abbot or prior. Conversion of life means, generally, that the monk convert himself to the way of a monk, which is death to self and to the world and life to God and to his work. A Christian monk is to be an instrument of God's work. Stability entails that the monk commit himself to the monastery for the remainder of his life, and so, upon death, will be buried at its cemetery. The vow of stability is unique to Benedictines. The solemn vows in other religious communities were eventually established as vows of obedience, poverty, and chastity. Poverty requires that they renounce any ownership of property or assets, except for items that were allowed to them by their superior (such as a religious habit, shoes, a cloak, etc.), and to live meekly, sharing whatever they might have with the poor. Chastity requires that since they were willing to dedicate their lives to God, they sacrificed the love between men and women and would not marry. Also, they give up any act of sexual conduct. To become a monk, one first must become a postulant, during which time the man lives at the monastery to evaluate whether he is called to become a monk. As a postulant, the man is not bound by any vows, and is free to leave the monastery at any time. If the postulant and the community agree that the postulant should become a monk, the man is received as a novice, at which time he is given his religious habit, and begins to participate more fully in the life of the monastery. Following a period as a novice, usually six months to a year, the novice professes temporary vows, which can be renewed for a period of years. After a few years, the monk professes permanent vows, which are binding for life. The monastic life generally consists of prayer in the form of the Liturgy of the Hours (also known as the Divine Office) and divine reading (lectio divina) and manual labor. Among most religious orders, monks live in simple, austere rooms called cells and come together daily to celebrate the Conventual Mass and to recite the Liturgy of the Hours. In most communities, the monks take their meals together in the refectory. While there is no vow of silence, many communities have a period of silence lasting from evening until the next morning and some others restrict talking to only when it is necessary for the monks to perform their work and during weekly recreation.  Monks who have been or will be ordained into Holy Orders as priests or deacons are referred to as choir monks, as they have the obligation to recite the entire Divine Office daily in choir. Those monks who are not ordained into Holy Orders are referred to as lay brothers. In most monastic communities today, little distinction exists between the lay brothers and the choir monks. However, historically, the roles of the two groups of monks within the monastery differed. The work of the choir monks was considered to be prayer, chanting the seven hours of the Divine Office and celebrating the Mass daily whereas the lay brothers provided for the material needs of the community by growing food, preparing meals, maintaining the monastery and the grounds. This distinction arose historically because generally those monks who could read Latin typically became choir monks, while those monks who were illiterate or could not read Latin became lay brothers. Since the lay brothers could not recite the Divine Office in Latin, they would instead pray easily memorizable prayers such as the Our Father or the Hail Mary as many as 150 times per day. Since the Second Vatican Council, the distinction between choir monks and lay brothers has been deemphasized, as the council allowed the Divine Office to be said in the vernacular language, effectively opening participation to all of the monks. Within western monasticism, it is important to differentiate between monks and friars. Monks generally live a contemplative life of prayer confined within a monastery while friars usually engage in an active ministry of service to the outside community. The monastic orders include all Benedictines (the Order of Saint Benedict and its later reforms including the Cistercians and the Trappists) and the Carthusians, who live according to their own Statutes, and not according to the Rule of St. Benedict proper. Orders of friars include the Franciscans, Dominicans, Carmelites, and Augustinians. Although the Canons Regular, such as the Norbertines, live in community, they are neither monks nor friars as they are characterized by their clerical state and not by any monastic vows. AnglicanismMonastic life in England came to an abrupt end when King Henry VIII broke from the Roman Catholic Church establishing the Church of England. He initiated the Dissolution of the Monasteries, during which all of the monasteries within England were destroyed. A few monks were executed, others fled to continental European monasteries, where they were able to continue their monastic life. Shortly after the beginning of the revival of the Catholic Movement in the Church of England, there was felt to be a need for a restoration of the monastic life. In the 1840s, Anglican priest John Henry Newman established a community of men at Littlemore near Oxford. From then on, there have been (re-)established many communities of monks, friars and other religious communities for men in the Anglican Communion. There are Anglican Benedictines, Franciscans, Cistercians, and in the Episcopal Church in the USA, Dominicans, as well as other monastic orders such as the Society of Saint John the Evangelist. Some Anglican religious communities are contemplative, some active, but a distinguishing feature of the monastic life among Anglicans is that most practice the so-called "mixed life". Anglican monks recite the Divine Office in choir daily, either the full eight services of the Breviary or the four offices found in the Book of Common Prayer and celebrate the Eucharist daily. Many orders take on external works such as service to the poor, giving religious retreats, or other active ministries within their immediate communities. Like Roman Catholic monks, Anglican monks also take the monastic vows of poverty, chastity, and obedience. In the early 20th century when the Catholic Movement was at its height, the Anglican Communion had hundreds of orders and communities, and thousands of religious followers. However, since the 1960s there has been a sharp falling off in the numbers of religious in many parts of the Anglican Communion. Many once large and international communities have been reduced to a single convent or monastery composed of elderly men or women. In the last few decades of the 20th century, novices have for most communities been few and far between. Some orders and communities have already become extinct. There are however, still several thousand Anglican monks working today in approximately 200 communities around the world. The most surprising growth has been in the Melanesian countries of the Solomon Islands, Vanuatu and Papua New Guinea. The Melanesian Brotherhood, founded at Tabalia, Guadalcanal, in 1925 by Ini Kopuria, is now the largest Anglican Community in the world with over 450 brothers in the Solomon Islands, Vanuatu, Papua New Guinea, the Philippines and the United Kingdom. Lutheranism Loccum Abbey and Amelungsborn Abbey have the longest traditions as Lutheran monasteries. Since the 19th and 20th century, there has been a renewal in the monastic life among Lutheranism. There are many present-day Lutherans who practice the monastic teaching of the Roman Catholic Church.[2] In American Lutheran traditions, "The Congregation of the Servants of Christ" was established at St. Augustine's House in Oxford, Michigan, in 1958 when some other men joined Father Arthur Kreinheder in observing the monastic life and offices of prayer. These men and others came and went over the years. The community has always remained small; at times the only member was Father Arthur.[3] During the 35 years of its existence over 25 men tested their vocations to monastic life by living at the house for some time, from a few months to many years, but at Father Arthur's death in 1989 only one permanent resident remained. At the beginning of 2006, there was 2 permanent professed members and 2 long-term guests. Strong ties remain with this community and their brothers in Sweden (Östanbäck monastery) and in Germany (Priory of St. Wigbert).[4] There is also the Order of Lutheran Franciscans, a religious community of friars and sisters within the tradition of the Evangelical Lutheran Church in America. MethodismSee also: Methodist Diaconal Order
Within the Worldwide Methodist Church there exist a number of diaconal orders. Like Roman Catholic canons and Jesuits, they are ordained (as deacons) but are also organised into a religious order. BuddhismSee also: Bhikkhu
 In Theravada Buddhism, bhikkhu is the term for monk. Their disciplinary code is called the patimokkha, which is part of the larger Vinaya. They live lives of mendicancy, and go on a morning almsround (Pali: pindapata) every day. The local people give food for the monks to eat, though the monks are not permitted to positively ask for anything. The monks live in monasteries, and have an important function in traditional Asian society. Young boys can be ordained as samaneras. Both bhikkhus and samaneras eat only in the morning, and are not supposed to lead a luxurious life. Their rules forbid the use of money, although this rule is nowadays not kept by all monks. The monks are part of the Sangha, the third of the Triple Gem of Buddha, Dhamma, Sangha. In Mahayana Buddhism, the term 'Sangha' strictly speaking refers to those who have achieved certain levels of understanding. They are therefore called 'community of the excellent ones' (Template:Lang-bo); however, these in turn need not be monks (i.e., hold such vows). Several Mahayana orders accept female practitioners as monks, instead of using the normal title of "nun", and they are considered equal to male ascetics in all respects. The Bhikkhus are only allowed 4 items (other than their robes): a razor, a needle, an alms bowl and a water strainer. In Vajrayana Buddhism, monkhood is part of the system of 'vows of individual liberation'; these vows are taken in order to develop one's own personal ethical discipline. The monks and nuns form the (ordinary) sangha. As for the Vajrayana vows of individual liberation, there are four steps: A lay person may take the 5 vows called 'approaching virtue' (in Tibetan 'genyen' < dge snyan>). The next step is to enter the monastic way of life (Tib. rabjung) which includes wearing monk's or nun's robes. After that, one can become a 'novice' (Pali samanera, Tib. getshül); the last and final step is to take all vows of the 'fully ordained monk' (gelong). This term 'gelong' (Tib. < dge long>, in the female form gelongma) is the translation of Skt. bikshu (for women bikshuni) which is the equivalent of the Pali term bhikkhuni; bhikkhu is the word used in Theravada Buddhism (Sri Lanka, Burma, Thailand).  Chinese Buddhist monks have been traditionally and stereotypically linked with the practice of the Chinese martial arts or Kung fu, and monks are frequently important characters in martial arts films. This association is focused around the Shaolin Monastery. The Buddhist monk Bodhidharma, traditionally credited as the founder of Zen Buddhism in China, is also claimed to have introduced Kalaripayattu (which later evolved into Kung Fu) to the country. This latter claim has however been a source of much controversy (see Bodhidharma, the martial arts, and the disputed India connection) One more feature about the Chinese Buddhist monks is that they practice the burning marks on their scalp, finger or part of the skin on their anterior side of the forearm with incense as a sign of ordination. In Thailand and Burma, it is common for boys to spend some time living as a monk in a monastery. Most stay for only a few years and then leave, but a number continue on in the ascetic life for the rest of their lives. In Mongolia during the 1920s, there were about 110,000 monks, including children, who made up about one-third of the male population,[5] many of whom were killed in the purges of Choibalsan. JainismOne of the most intense forms of Asceticism can be found in Jainism, one of the world's oldest religions. Jainism encourages fasting, yoga practices, meditation in difficult postures, and other austerities.[6] According to Jains, one's highest goal should be attaining Nirvana or Moksha (i.e., liberation from samsara, the cycle of birth and rebirth). For this, a soul has to be without attachment or self-indulgence. This can be achieved only by the monks and nuns who take five great vows: of non-violence, of truth, of non-stealing, of non-possession and of celibacy.  Most of the austerities and ascetic practices can be traced back to Vardhaman Mahavira, the twenty-fourth "fordmaker" or Tirthankara. The Acaranga Sutra, or Book of Good Conduct, is a sacred book within Jainism that discusses the ascetic code of conduct. Other texts that provide insight into conduct of ascetics include Yogashastra by Acharya Hemachandra and Niyamasara by Acharya Kundakunda. Other illustrious Jain works on ascetic conduct are Oghanijjutti, Pindanijjutti, Cheda Sutta, and Nisiha Suttafee. Full Jain monk in either Svetambara or Digambara tradition[7] can belong to one of these ranks:
These three are mentioned is the three lines of the Namokar Mantra. In the Digambara tradition, a junior monk can be a:
The Svetambar Terapanthi sect has a new rank of junior monks who are called samana. The nuns are called Aryikas in Digambar tradition and Sadhvi in the Svetambar tradition. Ascetic vows As per the Jain vows, the monks and nuns renounce all relations and possessions. Jain ascetics practice complete non-violence. Ahimsa is the first and foremost vow of a Jain ascetic. They do not hurt any living being, be it an insect or a human. They carry a special broom to sweep away any insects that may cross their path. Some Jain monks wear a cloth over the mouth to prevent accidental harm to airborne germs and insects. They also do not use electricity as it involves violence. Furthermore, they do not use any devices or machines. As they are without possession and attachment, they travel from city to city, often crossing forests and deserts, and always barefoot. Jain ascetics do not stay in a single place for more than two months to prevent themselves from becoming attached to any location. However during four months of monsoon (rainy season) known as chaturmaas, they continue to stay in a single place to avoid killing the life forms that thrive during the rains. Jain monks and nuns practice complete celibacy. They do not touch or share a sitting platform with a person of opposite sex. Dietary practicesJain ascetics follow a strict vegetarian diet without root vegetables. Shvetambara monks do not cook food but solicit alms from householders. Digambara monks have only a single meal a day. Neither group will beg for food, but a Jain ascetic may accept a meal from a householder, provided that the latter is pure of mind and body and offers the food of his own volition and in the prescribed manner. During such an encounter, the monk remains standing and eats only a measured amount. Fasting (i.e., abstinence from food and sometimes water) is a routine feature of Jain asceticism. Fasts last for a day or longer, up to a month. Some monks avoid (or limit) medicine and/or hospitalization due to their careful attention to body. Austerities and other daily practices Other austerities include meditation in seated or standing posture near river banks in the cold wind, or meditation atop hills and mountains, especially at noon when the sun is at its fiercest. Such austerities are undertaken according to the physical and mental limits of the individual ascetic. Jain ascetics are (almost) completely without possessions. Some Jains (Shvetambara monks and nuns) own only unstitched white robes (an upper and lower garment) and a bowl used for eating and collecting alms. Male Digambara monks do not wear any clothes and carry nothing with them except a soft broom made of shed peacock feathers (pinchi) and eat from their hands. They sleep on the floor without blankets and sit on special wooden platforms. Every day is spent either in study of scriptures or meditation or teaching to lay people. They stand aloof from worldly matters. Many Jain ascetics take a final vow of Santhara or Sallekhana (i.e., a peaceful and detached death where medicines, food, and water are abandoned). This is done when death is imminent or when a monk feels that he is unable to adhere to his vows on account of advanced age or terminal disease. Quotes on ascetic practices from the Akaranga Sutra as Hermann Jacobi translated it:[8][9]
VaishnavaMadhvaacharya (Madhvacharya), the Dwaita philosopher, established ashta matha (Eight Monasteries). He appointed a monk (called swamiji or swamigalu in local parlance) for each matha or monastery who has the right to worship Madhvacharya's murti of Lord Krishna by rotation. Each matha's swamiji gets a chance to worship after fourteen years. This ritual is called Paryaya and has been used also outside his sampradaya, e.g. in Gaudiya Vaisnava Radharamana temple in Vrindavan. Similar in appearance to Buddhist monks, brahmacari monks from the International Society for Krishna Consciousness (ISKCON), or Hare Krishnas as they are popularly known, are the best known Vaishnava monks outside India. They are a common sight in many places around the world. Their appearance—simple saffron dhoti, shaved head with sikha, Tulasi neckbeads and tilaka markings—and social customs (sadhana) date back many thousands of years to the Vedic era with its varnasrama society. This social scheme includes both monastic and lay stages meant for various persons in various stages of life as per their characteristics (guna) and work (karma). ISKCON started as a predominantly monastic group but nowadays the majority of members live as lay persons. Many of them, however, spent some time as monks. New persons joining ISKCON as full-time members (living in its centers) first undergo a three-month Bhakta training, which includes learning the basics of brahmacari (monastic) life. After that they can decide if they prefer to continue as monks or as married Grihasthas. Brahmacari older than fifty years (as per ISKCON rule) can become sannyasi. Sannyasa, a life of full dedication to spiritual pursuits, is the highest stage of life in the varnasrama society. It is permanent and one cannot give it up. A Sannyasi is given the title Swami. Older grihastha with grown-up children are traditionally expected to accept vanaprastha (celibate retired) life. The role of monastic orders in Indian and now also Western society has to some extent been adapted over the years in accordance with ever-changing social structures. See also
References
External links
|
Topic on Project talk:Sandbox/Structured Discussions test
In the following reply I will include a sample work-case taken from recent editing work I was involved in.
THIS IS A SAMPLE TAKEN FROM RECENT WIKIPEDIA WORK I WAS INVOLVED IN.
RFC
Hello Everyone,I prepared a table for Fields Medal page which,in my opinion,would help us to reach a consensus about edits which have to be done to the page.Of course,I did my best to make it as complete as I could.I think it can be replaced with existing table in the article.(I must greatly thank dcljr for proposing a new and excellent table format): RfC started 14:12, 17 August 2014 (UTC)
| Year | ICM Location | Medalists[1] | Affiliation (When Awarded) | Birthplace | Current/Last Affiliation | Citation |
|---|---|---|---|---|---|---|
| 1936 | Oslo, Norway | Lars Ahlfors | University of Helsinki, Finland | Finland | Harvard University, US[2][3] | "Awarded medal for research on covering surfaces related to Riemann surfaces of inverse functions of entire and meromorphic functions. Opened up a new fileds of analysis." |
| Jesse Douglas | Massachusetts Institute of Technology, US | United States | City College of New York, US[4][5] | "Did important work of the Plateau problem which is concerned with finding minimal surfaces connecting and determined by some fixed boundary." | ||
| 1950 | Cambridge, US | Laurent Schwartz | University of Nancy, France | France | University of Paris VII, France[6][7] | "Developed the theory of distributions, a new notion of generalized function motivated by the Dirac delta-function of theoretical physics." |
| Atle Selberg | Institute for Advanced Study, US | Norway | Institute for Advanced Study, US[8] | "Developed generalizations of the sieve methods of Viggo Brun; achieved major results on zeros of the Riemann zeta function; gave an elementary proof of the prime number theorem (with P. Erdös), with a generalization to prime numbers in an arbitrary arithmetic progression." | ||
| 1954 | Amsterdam, Netherland | Kunihiko Kodaira | Institute for Advanced Study, US | Japan | University of Tokyo, Japan[9] | "Achieved major results in the theory of harmonic integrals and numerous applications to Kählerian and more specifically to algebraic varieties. He demonstrated, by sheaf cohomology, that such varieties are Hodge manifolds." |
| Jean-Pierre Serre | University of Nancy, France | France | Collège de France, France[10][11] | "Achieved major results on the homotopy groups of spheres, especially in his use of the method of spectral sequences. Reformulated and exented some of the main results of complex variable theory in terms of sheaves." | ||
| 1958 | Edinburgh, UK | Klaus Roth | University College London, UK | Weimar Republic | Imperial College London, UK[12] | "Solved in 1955 the famous Thue-Siegel problem concerning the approximation to algebraic numbers by rational numbers and proved in 1952 that a sequence with no three numbers in arithmetic progression has zero density (a conjecture of Erdös and Turán of 1935)." |
| René Thom | University of Strasbourg, France | France | Institut des Hautes Études Scientifiques, France[13] | "In 1954 invented and developed the theory of cobordism in algebraic topology. This classification of manifolds used homotopy theory in a fundamental way and became a prime example of a general cohomology theory." | ||
| 1962 | Stockholm, Sweden | Lars Hörmander | University of Stockholm, Sweden | Sweden | Lund University, Sweden[14] | "Worked in partial diffential equations. Specifically, contributed to the general theory of linear differential operators. The questions go back to one of Hilbert's problems at the 1900 congress." |
| John Milnor | Princeton University, US | United States | Stony Brook University, US[15] | "Proved that a 7-dimensional sphere can have several differential structures; this led to the creation of the field of differential topology." | ||
| 1966 | Moscow, USSR | Michael Atiyah | University of Oxford, UK | United Kingdom | University of Edinburgh, UK[16] | "Did joint work with Hirzebruch in K-theory; proved jointly with Singer the index theorem of elliptic operators on complex manifolds; worked in collaboration with Bott to prove a fixed point theorem related to the "Lefschetz formula"." |
| Paul Joseph Cohen | Stanford University, US | United States | Stanford University, US[17] | "Used technique called "forcing" to prove the independence in set theory of the axiom of choice and of the generalized continuum hypothesis. The latter problem was the first of Hilbert's problems of the 1900 Congress." | ||
| Alexander Grothendieck | Institut des Hautes Études Scientifiques, France | Weimar Republic | Centre National de la Recherche Scientifique , France[18] | "Built on work of Weil and Zariski and effected fundamental advances in algebraic geometry. He introduced the idea of K-theory (the Grothendieck groups and rings). Revolutionized homological algebra in his celebrated "Tohoku paper"" | ||
| Stephen Smale | University of California, Berkeley, US | United States | City University of Hong Kong, Hong Kong[19] | "Worked in differential topology where he proved the generalized Poincaré conjecture in dimension n>=5: Every closed, n-dimensional manifold homotopy-equivalent to the n-dimensional sphere is homeomorphic to it. Introduced the method of handle-bodies to solve this and related problems." | ||
| 1970 | Nice, France | Alan Baker | University of Cambridge, UK | United Kingdom | Trinity College, Cambridge, UK[20] | "Generalized the Gelfond-Schneider theorem (the solution to Hilbert's seventh problem). From this work he generated transcendental numbers not previously identified." |
| Heisuke Hironaka | Harvard University, US | Japan | Kyoto University, Japan[21][22] | "Generalized work of Zariski who had proved for dimension" | ||
| John G. Thompson | University of Cambridge, UK | United States | University of Cambridge, UK [23] | "Proved jointly with W. Feit that all non-cyclic finite simple groups have even order. The extension of this work by Thompson determined the minimal simple finite groups, that is, the simple finite groups whose proper subgroups are solvable." | ||
| Sergei Novikov | Moscow State University, USSR | USSR | Steklov Mathematical Institute, Russia
Moscow State University, Russia |
"Made important advances in topology, the most well-known being his proof of the topological invariance of the Pontrjagin classes of the differentiable manifold. His work included a study of the cohomology and homotopy of Thom spaces." | ||
| 1974 | Vancouver, Canada | Enrico Bombieri | University of Pisa, Italy | Italy | Institute for Advanced Study, US[26] | "Major contributions in the primes, in univalent functions and the local Bieberbach conjecture, in theory of functions of several complex variables, and in theory of partial differential equations and minimal surfaces - in particular, to the solution of Bernstein's problem in higher dimensions." |
| David Mumford | Harvard University, US | United States | Brown University, US[27] | "Contributed to problems of the existence and structure of varieties of moduli, varieties whose points parametrize isomorphism classes of some type of geometric object. Also made several important contributions to the theory of algebraic surfaces." | ||
| 1978 | Helsinki, Finland | Pierre Deligne | Institut des Hautes Études Scientifiques, France | Belgium | Institute for Advanced Study, US[28] | "Gave solution of the three Weil conjectures concerning generalizations of the Riemann hypothesis to finite fields. His work did much to unify algebraic geometry and algebraic number theory." |
| Charles Fefferman | Princeton University, US | United States | Princeton University, US[29] | "Contributed several innovations that revised the study of multidimensional complex analysis by finding correct generalizations of classical (low-dimensional) results." | ||
| Daniel Quillen | Massachusetts Institute of Technology, US | United States | University of Oxford, UK[30] | "The prime architect of the higher algebraic K-theory, a new tool that successfully employed geometric and topological methods and ideas to formulate and solve major problems in algebra, particularly ring theory and module theory." | ||
| Grigori Margulis | Princeton University, US | USSR | Yale University, US[31] | "Provided innovative analysis of the structure of Lie groups. His work belongs to combinatorics, differential geometry, ergodic theory, dynamical systems, and Lie groups." | ||
| 1982 | Warsaw, Poland | Alain Connes | Institut des Hautes Études Scientifiques, France | France | Institut des Hautes Études Scientifiques, France
Collège de France, France |
"Contributed to the theory of operator algebras, particularly the general classification and structure theorem of factors of type III, classification of automorphisms of the hyperfinite factor, classification of injective factors, and applications of the theory of C*-algebras to foliations and differential geometry in general." |
| William Thurston | Princeton University, US | United States | Cornell University, US[33] | "Revolutionized study of topology in 2 and 3 dimensions, showing interplay between analysis, topology, and geometry. Contributed idea that a very large class of closed 3-manifolds carry a hyperbolic structure." | ||
| Shing-Tung Yau | Institute for Advanced Study, US | China | Harvard University, US[34] | "Made contributions in differential equations, also to the Calabi conjecture in algebraic geometry, to the positive mass conjecture of general relativity theory, and to real and complex Monge-Ampère equations." | ||
| 1986 | Berkeley, US | Simon Donaldson | University of Oxford, UK | United Kingdom | Imperial College London, UK[35] | "Received medal primarily for his work on topology of four-manifolds, especially for showing that there is a differential structure on euclidian four-space which is different from the usual structure." |
| Gerd Faltings | Princeton University, US | West Germany | Max Planck Institute for Mathematics, Germany[36] | "Using methods of arithmetic algebraic geometry, he received medal primarily for his proof of the Mordell Conjecture." | ||
| Michael Freedman | University of California, San Diego, US | United States | Template:FlagiconMicrosoft Station Q[37] | "Developed new methods for topological analysis of four-manifolds. One of his results is a proof of the four-dimensional Poincaré Conjecture." | ||
| 1990 | Kyoto, Japan | Vladimir Drinfeld | University of Kharkiv, USSR | USSR | University of Chicago, US[38] | "For his work on quantum groups and for his work in number theory." |
| Vaughan F. R. Jones | University of California, Berkeley, US | New Zealand | University of California, Berkeley, US[39], | "for his discovery of an unexpected link between the mathematical study of knots – a field that dates back to the 19th century – and statistical mechanics, a form of mathematics used to study complex systems with large numbers of components." | ||
| Shigefumi Mori | Kyoto University, Japan | Japan | Kyoto University, Japan[41] | "for the proof of Hartshorne’s conjecture and his work on the classification of three-dimensional algebraic varieties." | ||
| Edward Witten | Institute for Advanced Study, US | United States | Institute for Advanced Study, US[42] | "... his ability to interpret physical ideas in mathematical form is quite unique."[43] | ||
| 1994 | Zurich, Switzerland | Jean Bourgain | Institut des Hautes Études Scientifiques, France | Belgium | Institute for Advanced Study, France[44] | "Bourgain's work touches on several central topics of mathematical analysis: the geometry of Banach spaces, convexity in high dimensions, harmonic analysis, ergodic theory, and finally, nonlinear partial differential equations from mathematical physics." |
| Pierre-Louis Lions | Paris Dauphine University, France | France | Collège de France, France
École polytechnique, France[45] |
"... such nonlinear partial differential equation simply do not have smooth or even C1 solutions existing after short times. ... The only option is therefore to search for some kind of "weak" solution. This undertaking is in effect to figure out how to allow for certain kinds of "physically correct" singularities and how to forbid others. ... Lions and Crandall at last broke open the problem by focusing attention on viscosity solutions, which are defined in terms of certain inequalities holding wherever the graph of the solution is touched on one side or the other by a smooth test function." | ||
| Jean-Christophe Yoccoz | Paris-Sud 11 University, France | France | Collège de France, France[46] | "proving stability properties - dynamic stability, such as that sought for the solar system, or structural stability, meaning persistence under parameter changes of the global properties of the system." | ||
| Efim Zelmanov | University of California, San Diego, US | USSR | Steklov Mathematical Institute, Russia, | "For his solution to the restricted Burnside problem." | ||
| 1998 | Berlin, Germany | Richard Borcherds | University of California, Berkeley, US | South Africa | University of California, Berkeley, US[48] | "for his work on the introduction of vertex algebras, the proof of the Moonshine conjecture and for his discovery of a new class of automorphic infinite products" |
| Timothy Gowers | University of Cambridge, UK | United Kingdom | University of Cambridge, UK[49] | "William Timothy Gowers has provided important contributions to functional analysis, making extensive use of methods from combination theory. These two fields apparently have little to do with each other, and a significant achievement of Gowers has been to combine these fruitfully." | ||
| Maxim Kontsevich | Institut des Hautes Études Scientifiques, France | USSR | Institut des Hautes Études Scientifiques, France | "contributions to four problems of geometry" | ||
| Curtis T. McMullen | Harvard University, US | United States | Harvard University, US[51] | "He has made important contributions to various branches of the theory of dynamical systems, such as the algorithmic study of polynomial equations, the study of the distribution of the points of a lattice of a Lie group, hyperbolic geometry, holomorphic dynamics and the renormalization of maps of the interval." | ||
| 2002 | Beijing, China | Laurent Lafforgue | Institut des Hautes Études Scientifiques, France | France | Institut des Hautes Études Scientifiques, France[52] | "Laurent Lafforgue has been awarded the Fields Medal for his proof of the Langlands correspondence for the full linear groups
GLr (r≥1 ) over function fields." |
| Vladimir Voevodsky | Institute for Advanced Study, US | USSR | Institute for Advanced Study, US[53] | " he defined and developed motivic cohomology and the
A1-homotopy theory of algebraic varieties; he proved the Milnor conjectures on the K-theory of fields" |
||
| 2006 | Madrid, Spain | Andrei Okounkov | Princeton University, US | USSR | Columbia University, US[54] | "for his contributions bridging probability,
representation theory and algebraic geometry" |
| Grigori Perelman | None | USSR | Steklov Mathematical Institute, Russia[55] | "for his contributions to geometry and his revolutionary insights into the analytical and geometric structure of the Ricci flow" | ||
| Terence Tao | University of California, Los Angeles, US | Australia | University of California, Los Angeles, US[56] | "for his contributions to partial differential equations, combinatorics, harmonic analysis and additive number theory " | ||
| Wendelin Werner | Paris-Sud 11 University, France | West Germany | ETH Zurich, Switzerland[57] | "for his contributions to the development of stochastic Loewner evolution, the geometry of two-dimensional Brownian motion, and conformal field theory" | ||
| 2010 | Hyderabad, India | Elon Lindenstrauss | Hebrew University of Jerusalem, Israel | Israel | Hebrew University of Jerusalem, Israel[58] | "For his results on measure rigidity in ergodic theory, and their applications to number theory." |
| Ngô Bảo Châu | Paris-Sud 11 University, France | North Vietnam | Paris-Sud 11 University, France | "For his proof of the Fundamental Lemma in the theory of automorphic forms through the introduction of new algebro-geometric methods" | ||
| Stanislav Smirnov | University of Geneva, Switzerland | USSR | University of Geneva, Switzerland[60] | "For the proof of conformal invariance of percolation and the planar Ising model in statistical physics" | ||
| Cédric Villani | École Normale Supérieure de Lyon, France
Institut Henri Poincaré, France |
France | Lyon University, France
Institut Henri Poincaré, France[61] |
"For his proofs of nonlinear Landau damping and convergence to equilibrium for the Boltzmann equation." | ||
| 2014 | Seoul, South Korea | Artur Avila | Paris Diderot University, France
CNRS, France |
Brazil | Paris Diderot University, France
CNRS, France Instituto Nacional de Matemática Pura e Aplicada, Brazil[62] |
"is awarded a Fields Medal for his profound contributions to dynamical systems theory, which have changed the face of the field, using the powerful idea of renormalization as a unifying principle." |
| Manjul Bhargava | Princeton University, US | Canada | Princeton University, US[63][64] | "is awarded a Fields Medal for developing powerful new methods in the geometry of numbers, which he applied to count rings of small rank and to bound the average rank of elliptic curves." | ||
| Martin Hairer | University of Warwick, UK | Austria | University of Warwick, UK[65][66][67] | "is awarded a Fields Medal for his outstanding contributions to the theory of stochastic partial differential equations, and in particular for the creation of a theory of regularity structures for such equations." | ||
| Maryam Mirzakhani | Stanford University, US | Iran | Stanford University, US[68][69] | "is awarded the Fields Medal for her outstanding contributions to the dynamics and geometry of Riemann surfaces and their moduli spaces." | ||
| 2018 | Rio de Janeiro, Brazil[70] | n/a | n/a | n/a | n/a | n/a |
- ↑ Template:Cite web
- ↑ http://www.ams.org/notices/199802/comm-krantz.pdf
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ http://wdb.ugr.es/~geometry/seminar/files/talks/MMicallef20130207.pdf
- ↑ Template:Cite web
- ↑ Template:Cite book
- ↑ http://www.ams.org/notices/200906/rtx090600692p-corrected.pdf
- ↑ http://www.ams.org/notices/199803/comm-obit-spencer.pdf
- ↑ http://www.math.rug.nl/~top/lectures/delft.pdf
- ↑ Template:Cite web
- ↑ Template:Cite book
- ↑ http://www.robertnowlan.com/pdfs/Thom,%20Rene.pdf
- ↑ http://smai.emath.fr/IMG/pdf/matapli100_Hormander.pdf
- ↑ Template:Cite web
- ↑ http://upcommons.upc.edu/video/bitstream/2099.2/946/17/Poster05-AbelPrize-CV.pdf
- ↑ http://historicalsociety.stanford.edu/pdfmem/Cohen_P.pdf
- ↑ http://www.math.ucdenver.edu/~jloats/StudentCELEBS/Grothendieck_Trenkamp.pdf
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ http://www.ams.org/notices/200509/fea-hironaka.pdf
- ↑ Template:Cite web
- ↑ http://www.abelprize.no/c53860/binfil/download.php?tid=53792
- ↑ http://www.mi.ras.ru/~snovikov/998.pdf
- ↑ Template:Cite web
- ↑ Template:Cite book
- ↑ Template:Cite web
- ↑ http://www.abelprize.no/c57681/binfil/download.php?tid=57756
- ↑ http://web.math.princeton.edu/WebCV/FeffermanCV.pdf
- ↑ http://www.ams.org/notices/201210/rtx121001392p.pdf
- ↑ http://users.math.yale.edu/public_html/People/gam3.html
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ http://www.doctoryau.com/yau_cv.pdf
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ http://celebratio.org/cmmedia/essaypdf/19_main_3.pdf
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ http://www.sns.ias.edu/~witten/CurrentCV.pdf
- ↑ http://www.mathunion.org/ICM/ICM1990.1/Main/icm1990.1.0031.0036.ocr.pdf
- ↑ https://www.math.ias.edu/files/bourgain/CVBourgain.pdf
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ http://www.ime.usp.br/~grishkov/papers/CV.Zelm..pdf
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ http://abel.math.harvard.edu/~ctm/vita/resume.pdf
- ↑ Template:Cite web
- ↑ http://www.math.ias.edu/~vladimir/Site3/home_files/mitcv12.pdf
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ http://www.heidelberg-laureate-forum.org/blog/laureate/bao-chau-ngo/
- ↑ http://www.unige.ch/~smirnov/
- ↑ http://cedricvillani.org/wp-content/uploads/2012/10/cv-2012.pdf
- ↑ https://www.imj-prg.fr/~artur.avila/cur.pdf
- ↑ http://www2.maths.ox.ac.uk/cmi/library/research_award/Bhargava/CV.pdf
- ↑ http://www.mathunion.org/fileadmin/IMU/Prizes/2014/news_release_bhargava.pdf
- ↑ http://www.mathunion.org/fileadmin/IMU/Prizes/2014/news_release_hairer.pdf
- ↑ http://www.hairer.org/cv.pdf
- ↑ http://homepages.warwick.ac.uk/~masdbd/cv.pdf
- ↑ http://www2.maths.ox.ac.uk/cmi/library/annual_report/ar2008/08Interview.pdf
- ↑ Template:Cite web
- ↑ Template:Cite web
